Official GRE Problem-Solving Practice Questions

The correct answer is (C).

At its heart, this question is just a weighted-average problem comparing the ages of two different groups. The error students often make here, even if they ultimately get the question right, is one of approach (i.e., failing to select the most efficient solution methodology).

The traditional way to solve this problem is to create an algebraic equation, but it is both time-consuming and unnecessary. It’s much quicker to use a mapping technique for weighted averages.

If the average age were 38.5, that would mean there are an equal number of people in groups G and H—because 38.5 is the midpoint between the two averages. This scenario is shown below:

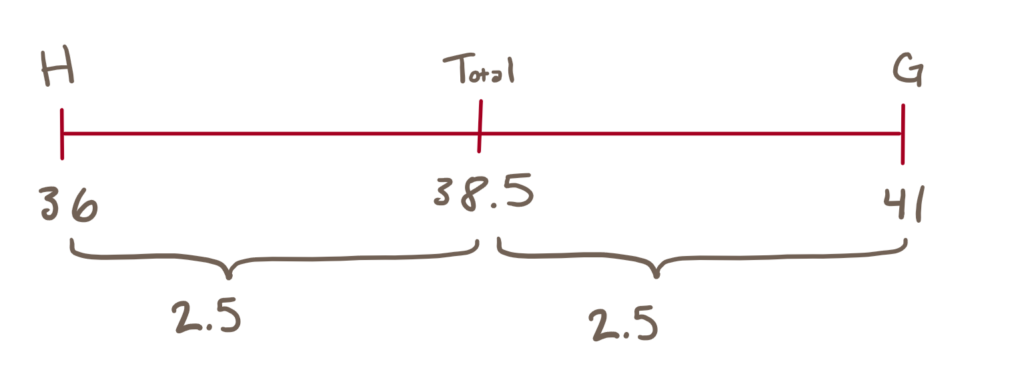
The distances between the individual groups and the combined average form the ratio of each group (here the relative distances are 2.5:2.5, which is a ratio of 1:1). The answer in this scenario would clearly be `1/2`.

In this problem, though, you actually have the scenario mapped out below:

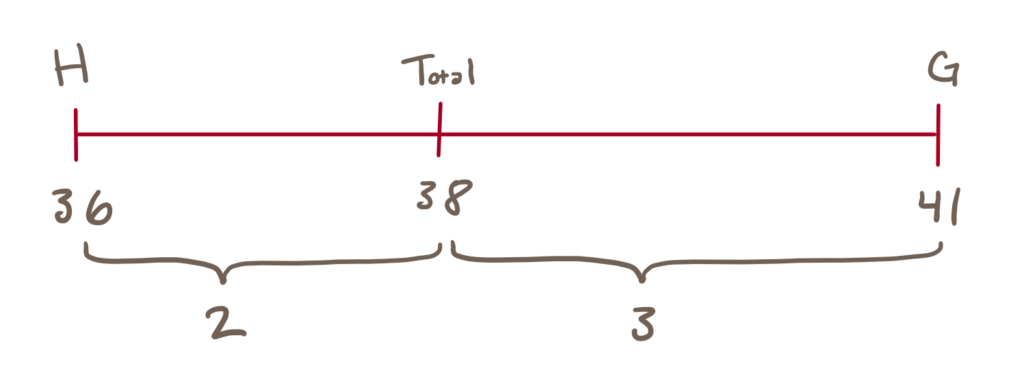
It should be clear that there must be more people in group H than in group G because the average is closer to 36 than it is to 41. To create the ratio of group H to group G you must invert the distances between the individual groups and the overall average to get the ratio of `H/G : 3/2`.

However, in this case, the question is asking not for the ratio of group H to group G, but for the ratio of group H to the total. Since the two distances add up to 5, this ratio would be `H/text(Total) : 3/5`, which is answer choice (C).

Important: When using this strategy, don’t forget to invert the distances and give the initial ratio in reverse. You can always double-check that you have the ratio correct by ensuring the component that’s closer to the overall average is represented by the larger element in the ratio. The ratio skews closer to the component that carries more weight!

Before jumping headfirst into any GRE problem-solving question, take a moment to consider your approach.

This is a clear spot where you can gain a minute or more over other test-takers who resort to algebra instead of mapping. You may not always make the right choice initially, but as you complete more and more GRE practice problems, your decision-making skills will become that much sharper.

Once you get comfortable with this approach, you can often answer these questions very quickly with little to no written work.

The correct answer is (D).

This is what’s known as a “limit” question; it asks you to determine, not the exact value of something, but its maximum or (in this case) minimum possible value. Students often find these questions fairly abstract and unapproachable, but they shouldn’t be, if approached with the right tools.

Here, there are some key details that will enable us to arrive at our solution:

First, the maximum value any of these variables can have is 110.

Second, since we have 5 variables that average out to 100, we know that these variables add up to 500.

Third, the use of ≤ (less than or equal to) signs means that these values don’t have to be unique. They could very well all be equal to 100, for example.

We want to make r as small as possible while still ensuring the values add up to 500. Therefore, we want to make every other value as big as possible—and there’s nothing to say they can’t all be equal to the maximum value of 110.

At this point, one approach is to simply solve the problem algebraically:

`r+s+t+u+v=500`

`r+4(110)=500`

`r+440=500`

`r=60`

This gets us to the right answer, but there is a second way to think about the problem that is generally more efficient: the “over-under method.”

This method involves looking at the difference between the maximized values (110) and the average value (100).

In this case, each maximized value is 10 over the average. There are 4 of these values, so the total “overage” or surplus is 40. The one remaining value, r, therefore needs to be 40 under the average to balance the other values out. That is, of course, 60.

For this particular question, the time we save by dodging the algebra might be insignificant, but as we get into more difficult “limit” questions that would require more extensive algebra, the over-under method stands to save us a great deal of time.

The correct answer is (C).

A challenging GRE quant question usually doesn’t require more advanced or time-consuming calculations than an easier question. But it will often trick you into wasting your time on such calculations if you don’t spot the shortcuts.

This question is a great example of that dynamic. There are a number of ways to get to the right answer here. We could use some fairly long-winded algebra that would get us the right answer, at the expense of much more of our precious time than we can afford to spend on one question.

We could backsolve, trying out the different options provided until we find the one that works. This also risks involving a bunch of calculations, depending on how quickly we happen to land on the right answer.

The smart way involves looking logically at clues in how the question is constructed. Remember, GRE questions are always designed in such a way that the right answer can be inferred quickly—if you know how. They are testing, not your ability to do very complicated math, but your ability to approach quantitative problems efficiently.

Look at the range of answers provided. They cover quite a wide numerical range, but you may notice that options (C) and (D) are clustered much closer together than any of the others. This is important because the options you’re given in these multiple-choice questions are not random; they are part of the information you’re working with.

If we try simply dividing the money equally between the two accounts, we know that the total interest earned will be at the exact midpoint of the two accounts’ interest rates—at 4%. 4% of $6,400 is $256—that is, option (D), one of the two suspiciously clustered answers in our list.

But we know that if the two accounts earned different interest rates and yet both ended up with the same amount of interest after a year, the money of course wasn’t equally divided.

So what? We’ve eliminated (D) as a possible answer, and we now have four other possible answers? Well, no. We’ve actually gained all the information we need.

Logically, we see that we have to put more money into the 3% account in order to earn the same interest as on the 5% account. That moves our average interest rate below 4% and thus necessarily lowers the total interest we will earn—so clearly, option (E), as a higher amount, is eliminated.

Of the other three options, we should quickly realize that (A) and (B) are much too low to be plausible answers—they’re in fact both less than 3% of $6,400, whereas we know our answer must represent somewhere between 3% and 4% interest on that amount.

Importantly, even if (A) and (B) weren’t completely outside the range we need, we should still land on the right option based on the ratios involved. That is, 3% is a little more than half of 5%; therefore, a little more than half of the money must be in the 3% account; therefore, we need something a little less than 4%—i.e., a little closer to 3% than it is to 5%—and pick option (C).

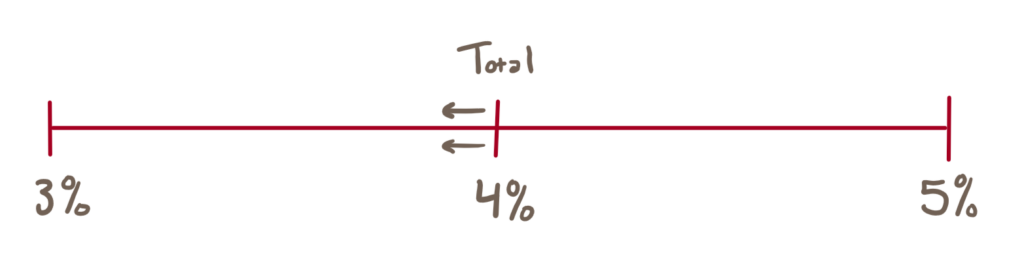
The point to take away from this explanation is that all of the wrong answers can be easily eliminated with straightforward logic; the precise calculations don’t need to be done. If we can quickly infer that the weighted average interest rate cannot be exactly 4% but must be only a little way below it, we can immediately see that only option (C) fits this description.

As always, this is not just about getting the correct answer, but about finding the path of least resistance. The question appears open-ended, but if we develop familiarity with the tricks GRE questions play, and flexibility in our approach, it doesn’t need to take long at all.